Les objets 3D
Introduction
Comme ce chapitre porte bien sont nom...
Nous allons avoir besoin de 2 différents objets près pour un affichage 3D sous OpenGL:
- La sphère
- Le cube.
Pour y parvenir, nous allons utiliser la conception d'objet en partant de ceci:
Pour la sphère : la sphère est une pécialisation d'un sphéroïde qui est lui même une spécialisation des quadriques qui sera une spécialisation de Objet3d. Ce qui nous donne :
Objet3d - > quadrique - > sphéroïde - > sphère
De même pour le cube, ce qui nous donne :
Objet3d - > polyèdre - > hexaèdres - > parallélépipèdes - > cube
Nous allons simplifier le contenu de ces classes. Certains contrôles ne seront pas effectués, le but n'étant pas de développer entièrement ce genre de classes ici !
Equation d'une ellipsoïde
Pour dessiner une sphère sous OpenGL, il nous faut l'équation de l'ellipsoïde.
Comme vous le savez certainement, tout le monde sait celà non ? (Sinon, comme moi, vous pouvez la trouver sur des sites spécialisés ou encore sur Wikipédia), l'équation d'une ellipsoïde est:
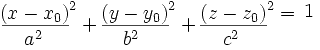
Avec x0, y0 et z0 les coordonnées du centre de l'ellipsoïde, a le rayon en x, b le rayon en y et c le rayon en z. x, y et z étant les coordonnées d'un point quelconque sur l'ellipsoïde.
Pour nous simplifier la tâche, les objets que nous allons dessiner seront tous de centre O(0,0,0). En fait, il sera plus simple de déplacer le centre de notre ellipsoïde via une translation sous OpenGL. Nous nous contenterons donc de préparer un objet 3D près à subir toutes les tranformations par la suite via les commandes OpenGL (Homotéthie, translation, rotation)
L'équation de notre ellipsoïde pourra donc se simplifier:
Après triturations de cette belle équation (dont je vous ferais grâce de la démonstration...), vous pouvez obtenir ceci:
![]()
![]()
![]()
Avec pour nous, x0, y0 et z0 qui seront nulles...
Equation d'une sphère
Une sphère est donc une ellipsoïde particulière. Nous avons a = b = c. Il s'agit du rayon de la sphère que l'on notera r.
L'équation de la sphère est donc après une petite manipulation (que là je peux très facilement vous démontrer tellement c'est simple !):
![]() (Source Wikipédia)
(Source Wikipédia)
qui nous donne:
![]()
![]()
![]()
(Source Wikipédia)
Les vecteurs normaux dans une sphère
Si nous voulons gérer de la couleur, nous aurons besoins de calculer des vecteurs normaux à un plan particulier.
Dans le cas d'une sphère, pour un vertex donné, le plan serait celui qui passe par ce vertex et qui ne passe pas par les autres vertice de notre sphère.
Ou encore, ce plan est le plan qui passe par notre vertex et qui est perpendiculaire à la droite formée par notre vertex et le centre de notre sphère. Or le vecteur à calculer pour notre vertex qui est normal à notre plan passe aussi par le vertex et sera donc parallèle à notre droite...
Le vecteur normal doit être de norme = 1. Si nous regardons bien la formule de notre sphère, si r = 1, tous segments tracés entre le centre de notre sphère et un point de la sphère auront donc une taille de 1 et pourront servir de coordonnées pour notre vecteur normal !
Pour calculer les vecteurs normaux, il suffira de calculer x, y et z avec un r = 1.
Pour calculer les points de notre sphère, il restera alors à multiplier par r les valeurs trouvées précédements.
Les vecteurs normaux dans une ellipsoïde
Notre vecteur pourra toujours être calculé à partir des coordonnées de notre point et du centre (même principe que la sphère). Mais il n'est alors plus question ici de mettre les rayons à 1. Car nous aurions alors à faire à une sphère et pas une ellipsoïde quelconque !
La norme de notre vecteur ne pourra donc pas être à 1...
Rendre unitaire les vecteurs normaux
Il va donc nous falloir rendre unitaire les vecteurs normaux pour chacuns des points calculés. La première solution pourra être d'utiliser la fonction glNormal (voir couleurs et lumières). Seulement, cela nous oblige à utiliser l'option GL_NORMALIZE...
Or on va éviter cela. Comment, en rendant nous même unitaire notre vecteur !
Pour cela, rien de plus simple, il suffit de calculer la norme de notre vecteur puis de diviser x, y et z par cette norme !
Pour rappel, soit:
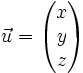
alors
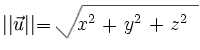
Cette fonction pouvant servir à tous les objets 3D, elle sera développée dans la classe objet3D et indiquera automatiquement à OpenGL le vecteur normal après l'avoir rendu unitaire.
Préparer nos objets
Assez de mathématique, maintenant que nous savons comment calculer les formes et définir les vecteurs normaux, il ne nous reste plus qu'à créer une ou plusieurs méthodes pour indiquer à OpenGL comment dessiner ces objets.
L'idée va être la suivante.
Après avoir initialisé OpenGL, il suffira de créer une instance d'un objet 3D en passant les valeurs nécessaires pour calculer l'objet 3D.
Ce n'est pas à nos instances de dessiner les objets à l'écran, mais à OpenGL. Nous nous contenterons donc à ce moment là de préparer l'objet et ces vecteurs normaux et nous les mettrons dans une display list.
Lorsque notre fenêtre aura besoin de redessiner son contenu, nous pourrons faire toutes les transformations que nous souhaitons avant de demander à l'instance de notre objet comment dessiner cet objet. Pour cela, il suffira d'appeler la méthode afficher() qui fera alors appel au contenu de la display list (d'où gain de vitesse, puisqu'il ne faudra pas tout recalculer à chaque fois). Ce contenu qui sera renvoyé ainsi à OpenGL pour affichage à l'écran.
Clonage d'un objet sous OpenGL
Ce principe permettra aussi d'utiliser l'idée de "clonage" d'un objet. Le fait d'avoir une instance d'un objet 3D n'empêchera pas d'avoir cet objet dessiné n fois sous OpenGL. Par contre, du moins si vous restez propre, la modification de la couleur de notre objet 3D provoquera le changement automatique de la couleur de tous ces clones. Si vous voulez que la couleur soit différente entre clone, vous pourrez aussi prévoir la désactivation de la gestion couleur automatique par notre instance. cela permettra alors à chaque clone d'avoir sa propre couleur que l'on définirai via OpenGL en utilisant glColor. Il est vrai que la couleur est déjà liée au dessin de l'objet.
Retour à la Boing Ball
La boing ball est donc une sphère dans laquelle il faudra afficher des carrés blancs et des carrés rouges. Comme il s'agit d'une sphère pariculière, le code se retrouvera directement dans la classe sphère.
Les codes pour les quadriques
Les .CPP:
Les .H correspondants:
et puis un exemple pour essayer tout cela:
Lors de la création du projet correspondant, il faudra ajouter les librairies OpenGL.
Le cube
Concernant le cube, rien de bien difficile, comme nous l'avons déjà vu dans OpenGL, les bases - Couleurs et lumières
Remarque, je fais ici un cube de manière très simple, une face étant composée de 4 vertice. Mais si vous voulez utiliser un spot avec une lumière spéculiaire, le rendu ne sera pas terrible (cf. fin du chapitre sur les spots), il faudra alors modifier le code pour pouvoir dessiner - via un pas - une face avec plusieurs vertice (composant elles-mêmes plusieurs petites faces dans notre face).
Je parle de cube, mais n'oublions les parallélépipèdes, ...
Pour rappel, le découpage en objet sera:
Objet3d - > polyèdre - > hexaèdres - > parallélépipèdes - > cube
Les classes polyèdre et hexaèdre ne contiennent (presque) rien pour le moment (inutile pour notre exemple). A compléter si nécessaire par la suite.
Les codes pour les polyèdres:
Les .CPP:
Les .H:
Un exemple:
Lors de la création du projet correspondant, il faudra ajouter les librairies OpenGL.
