Matrice identité
Voici la représentation d'une matrice identité
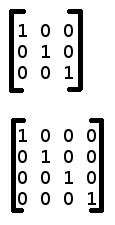
Il s'agit tout d'abord de matrices homogènes (car composées de coordonnées homogènes). La première matrice sera utilisée en 2D, la seconde en 3D. D'où les 3x3 ou 4x4 colonnes car les coordonnées d'un point ne sont pas déterminées de façon cartésiennes (x,y) en 2d ou (x,y,z) en 3d mais de façon homogènes (x,y,w) ou (x,y,z,w) donc en ajoutant une information w, ce que permet justement OpenGL avec son vec4.
La matrice cartésienne d'identité va permettre de conserver les coordonnées x, y et z en la multipliant avec les coordonnées d'un vecteur:
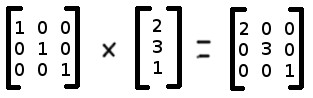
Si vous ajoutez une 4 ième dimension w à la matrice "identité" pour obtenir une matrice homogène, vous pourrez utiliser un xtranslation,ytranslation et ztranslation:
D'où la matrice suivante: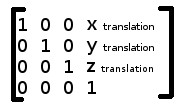
En reprenant le point aux coordonnées cartésiennes (2, 3, 1) soit en coordonnées homogènes (2, 3, 1, 1)
Vous obtenez un point qui après addition des éléments de la matrice provoquera une transalation de celui-ci:
A(2 + xtranslation, 3 + ytranslation, 1 + ztranslation)
En résumé, les matrices homogènes combinées avec les matrices identités vont permettre d'effectuer des transformations par simple multiplication de matrices. Les GPU vont en remercieront !